Is the universe a calculator?

This last week I woke up at about 4am and actually got up out of bed, to write in my notebook, some questions that follow from Newtonian space-time metaphors. I mention this getting up to write down, because it was quite complex sleep thinking, and usually when I think at 4am I tend to remain asleep. My waking hours when I write are the result of great pressure at depth like an artesian basin, a turbulent source of conscious, semi-conscious, subconscious and unconscious movements. I may think I can just write easily but there is a lot of prep going on.

While reading Julian Barbour's The Janus Point I became aware how old my understanding of the physics of the universe is. And I had never had the higher mathematics to follow disputations about which mathematical methods gives better descriptions of physics. I almost instantly resort to metaphor.

String theory, membranes, monadology… sure.

In any case, will the mathematics alone tell us which is more accurate? No, it only helps us measure our testing technologies, and bed down the repetitive nature of successful scientific progress.

So reading the Janus Point was more than a refresher, even without signing on for the main message.

See for my reaction review while reading Barbour's book, but also  A wonderful straightedge of a book about about Lorraine Daston's Rules: A Short History of What We Live By, and a general post on proportion, for my context at the moment.

Basically all measures or rules are a metaphor. I say this partly because there are so many mathematics out there that any particular type or school or area is unlikely to have anything to do with your focus or study. It is nnot like oh yes, methematics, just need to turn the tap on and it will explain X. A lot of science is testing which bits better map the question under investigation, both repeatedly and predictive testing-ly. "Better" is not a objective term, even if we think objectivity is better.

You’ll need metaphor to sort through or triage which mathematics you’ll use at first go. the iterate as we say nowadays. Sometimes this is called reason, though this perhaps gives too much weight to ratio.

The basic criticism of Newtonian notions of space-time is that it is not inclusive enough, as it seperates out the measurement or at least the frame of the universe to some crystalline structure that the universe expands through or occupies. Like a wave expanding on the surface of a pool of water.

It ignores the fact that we are measuring the universe using things of the universe (including metaphor and how we organise our measurements) and cannot step outside of if like we imagine stepping outside of a box or prison cell.

Apparently we can approach the mind of god by doing this, which is in part a metaphor for getting a point of view outside the universe, like one becomes the Newtonian crystalline space-time grid itself, or something?

But here we are.

Anyway, when Einstein comes along we get a new view which incorporates Newtonian descriptions (which have been tested and are predictive as far as they go) and adds some plasticity to the crysalline space-time, and so brings some of it back into the universe, mostly by way of gravitation.

Gravity can bend 'space-time', such that the wave expanding on the surface of the pool, does so on a volume of water that woggles according to mass. An effect which is great in expansive influence but drops off quickly in actual strength, i.e. it is locally important and universally available (I remember reading once that there is some maths in membrane theory that accounts for this by assuming the full force of gravity drops off by comparison with other forces because gravity leaks out across other membranes/universes/dimensions, and say, electro-magnetisim, leaks out not so much.)(This other dimensions allow imaginary distance to have effect.)

Einsteinian space-time is a sort of hybrid wherein the outside measure or ruler is placed into extra dimensions in the universe but not directly available to us. They structure the universe, and there is some mathematics to test how accurate all this is. 

Barbour's point on this (regardless of his Janus point distinctions) is that in this later physics of the 20^th century the Newtonian space-time ruler that we lay outside what we seek to measure has not been entirely exorcised. Nor brought inside the tent. That we still seek to measure the universe with an imaginary ruler which we place outside the universe we are trying to take our measure off.

Now it is not that these are wrong-headed, and so everything is wrong, merely that the ladders we have use to get here may not help us gain any further height until we have discarded them, as ladders, or rulers.

Regarding the universe as a sub-box of the space-time grid works well enough, Barbour says, for steam engines and thermodynamics, but may lead us astray in more cosmological questions. 

Barbour illustrates this by considering the expansion of the universe not in relation to some-(thing) exterior/extrinsic to the universe like a space-time grid, if gravitationally sensitive, but in the relations between bits/particles/points within the universe itself. I will attempt to describe this subtlety.

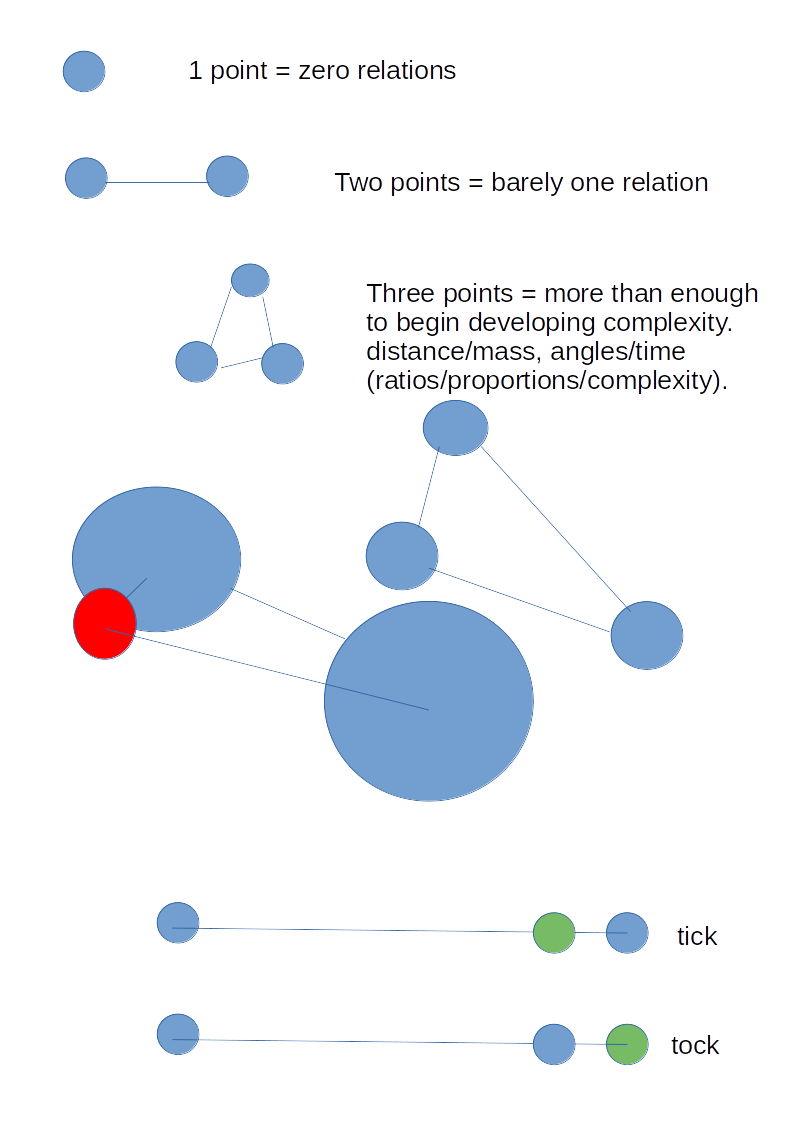
I’ll begin by counting and then getting confused, I mean, complicated. (This is the 4am stuff). The following image is added to help with its 'explanation' below.

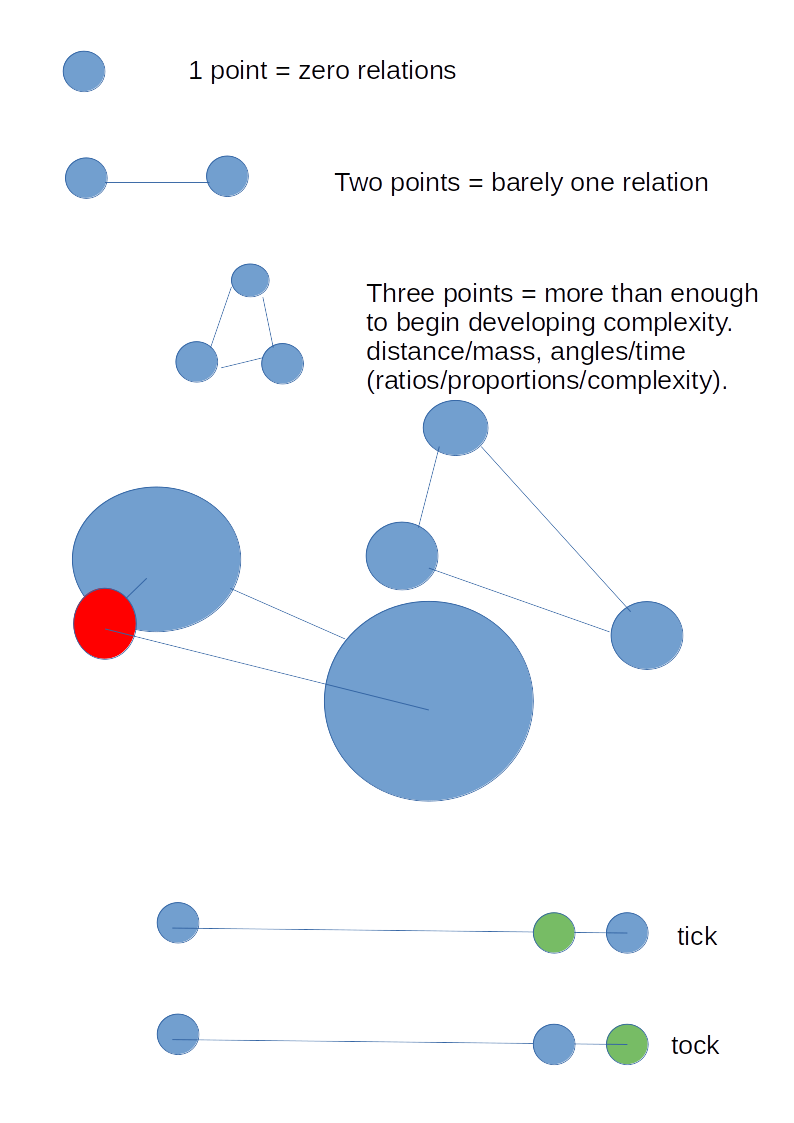
1. One point has no relations, therefore no ratios and no proportions. 1=0
2. Two points have one relation. It is barely a ratio, and there is no proportion. 2=1
3. Three points have at least 3 relations. This gives two to three proportions. 3=many

In ③ how many proportions depends on the practical differences between the points. If they are gravitational masses and they all have the same mass, then for practical purposes there are 3 relationships, but if there is a difference in mass sizes then there are more noticeable permutations. I.E. the logical number, the potential number of relations, and the practical number are not always the same. Already mathematics and the universe are at odds.

It is the number of relations that are important not the number of particles/bits bouncing around (unless that affects relations). If we replace those relations with a space-time grid or box we miss an opportunity.

Question 1. how logical is the universe?

Thus, we can argue about the mass/distance distinction/relations here as well, because there is a relationship with distance as measured, not against a space-time grid, but, in/with the relations of the other points in the system under consideration. Their ratios are measured in proportion to everything other in the system. If gravity's power did not drop off, then distance would not exist. 

Question 2. I guess where gravity's power = zero (or distance = zero) that is near the edge of the universe (or no universe)?

At the same distance from a point, different sized masses will have different relations with that first point, while at different distances with the same sized masses will have the same relations or effect on that first point.

In a space-time grid, the grid is bent by Einstein to match these observed effects, i.e. the measure is bent to account for these complexities. The 'rule' of objectivity we have placed outside the universe (which boxes it) is bent to account for reality or observed truths. Such is the mind of god for these people; certainly a god-emporer would agree.

Objectivity can lead to megalomania as much as it can to truth among friends discussing life's questions.

There is no need to bend anything if there is no grid. It all just woggles around in relation to all its bits. The universe is a blob of itself. The straight lines between points do not array nor argue with any space-time crystalline grid. The straight lines are part of the tensegrity of the universe.

And this does not even consider the angles between the relations, which physicists skip to almost immediately. (I get lost here). But they may not acount for much when the distances are tiny, I mean if there are no distances then there are no angles to worry about just yet. Of course the further away one is the less a change in angle will affect proportions. Maybe gravity is keen on ignoring angles just like I am.

Maybe that is the difference and is why gravity’s influence is universally pervasive but weaker than the others.

Should these gravitational points have other qualities besides just gravitation, and/or other qualities and no gravitational oomph, then the number of relations and thus ratios, and thus proportions (meta-ratios) between all of them increases at an increasing rate.

And then when we factor in the actual number of bits/point/particles/waves in the universe and we see how complicated it gets. The mind is blown. Much like big bang perhaps.

Barbour reckons that the expansion of the universe, and its relative bendiness is because of these relations, that the Newtonian space-time crystal is a distraction, that by boxing us into a local view as universal, we will not understand the relationship between entropy and complexity. 

My question is if, we are misguided to use an imaginary ruler, that is independent of the universe to take our measure from, like Newtonian space-time, and it is in this mindset  Barbour says, which allows us to mistakenly think the universe is a box or a bag in that space-time crystal, so, are we also mistaken to think that the universe calculates in the same way our mathematics does (I grant that we do do that in the universe). I.E. the model is the universe to some degree we cannot differentiate out.

Question 3. Does the universe calculate?

Does the universe calculate? Or do we just find the mathematics that calculates in the way the universe moves. Will our mathematics ever map nicely to all physics? If mathematics itself suffers from incompleteness, what hope is there we can map from it to the universe’s myriad relations, their ratios and their proportions of distinction?

Barbour says all science is ratios. (I'd add that constants are then just magical noise).

We are happy to admit that we are imperfect and so we may never be able to get physics all done, but can we admit that perhaps it is not possible by any measure?

Question 4. Further, if the universe does indeed calculate, does the "halting problem” apply? Does the universe expand because it 'calculates' without end?

Question 5. Does complexity increase because the system is Gödelianly 'incomplete'? Inflation = gaps accruing inthe system algorithmically expands the number of relations both nominally & practically?

More calculations begat more points begats more relations, more ratios, more proportion, more calculations? Thus the universe continues to expand/inflate if universe=calculation:ratio:proportion.

It is with this sort of thing in mind (I am guessing, because | maths) that Barbour proposes that entropy is only a local effect, because complexity increases at the largest scale, and that the heat-death of the universe may well be an over-rated fear.

He also calls that increase in complexity entaxy, in the meaning ‘towards order’. Here order is emergent, and not a top down command from the mind of god in the space-time crystal of power, and is all-dependant on the increasing number of relations, becoming ratios, becoming proportions, flows, gradients and life itself.

I was going to mention all those theogonies which argue about whether god is in or outside of the universe, or at least the human bit of the universe, but this post is already too long.

Barbour, Julian. “A History of Thermodynamics,” http://www.platonia.com/A_History_of_Thermodynamics.pdf.

Barbour, Julian B. The Janus Point: A New Theory of Time. First edition. New York: Basic Books, 2020.

You can leave comments on  substack while i work on disqus plugin issues here. Or email me from details on the about page.